How to Win a Data Science Competition: Learn from Top Kagglers-Week 3 강의 내용 정리

 

정리 글 항목 

• Week 1 정리
• Week 2 정리

Week 3에서 배우는 것

• Metric Optimization
• Metrics이란
• Regression, Classification Metric
• 각 Metric별 최적화 기법
• Mean Encoding

Metric Optimization

Metrics

학습에 따른 Decision Boundary 예시(출처)

• 학습을 통해 목표를 얼마나 잘 달성했는지를 나타내는 척도
• 선택한 Metric에 따라 최적의 Decision Boundary가 달라짐
• 학습을 통해 선택한 Metric에 최적화된 결과를 얻을 수 있음
• Competition에서 순위를 매기는 데 사용되며 Metric에 따라 모델 성능이 다를 수 있음

Regression Metrics

MSE, RMSE, R-squared

Mean Squared Error(MSE) 식

Root Mean Squared Error(RMSE) 식

Regression 결과(파란색 선)와 실제 값(보라색 원)의 차이(빨간색 선)

• MSE : 예측값과 실제값의 차이들을 합하여 제곱한 것
• RMSE : MSE 값에 Root 값을 씌운 것
• 큰 오류값에 대해 크게 패널티를 주는 장점
• 특이값에 영향을 덜 받음

R-squared Error 식

R-squared Error와 MSE와의 관계

Regression 결과와 실제값으로부터 R-squared Erorr 구하는 방법(출처)

• R-squared Error : Regression Line으로부터의 MSE와 데이터의 Average 값으로부터의 MSE를 이용하여 구한 에러
• Sum of Squared Error(SSR) : Regression Line으로부터의 MSE
• Sum of Squares Total(SST) : 데이터의 Average 값으로부터의 MSE

MAE

Mean Absolute Error(MAE) 식

• MAE : 예측값과 실제값의 차이들의 절대값으로 평균 낸 것
• 직관적으로 설명가능한 것이 장점
• 특이값이 있는 경우 Robust함 -> Outlier가 많은 데이터를 사용해야 될 때 Metric으로 사용하기 좋음
• MSE, RMSE는 제곱을 하기에 Outlier가 있으면 Error값이 급격하게 커지기 때문

(R)MSPE, MAPE

Mean Squared Percentage Error(MSPE) 식

Mean Absolute Percentage Error(MAPE) 식

• 단순 차이만으로 알 수 없는 Error값을 구하는데 사용
• 10개 중에 9개를 적절히 예측한 것과 1000개 중에 999개를 적절히 예측한 것을 가정
• MAE와 MSE는 전자와 후자가 동일한 에러값
• MSPE와 MAPE는 비율을 이용하여 전자, 후자를 다르게 계산
• MAPE: 예측값과 실제값의 차이의 비율을 구하여 나타낸 것
• 실제값이 1보다 작을수록 분모가 작아져 MAPE값이 무한대로 갈 수 있는 단점 존재

(R)MSLE

Mean Squared Log Error(MSLE) 식

Root Mean Squared Log Error(RMSLE) 식

• MSLE : MSE에 log를 적용한 값
• RMSLE : MSLE 값에 Root 값을 씌운 것
• RMSE보다 좋은 점
• 특이점에 영향을 덜 받음
• 상대적 Error를 측정
• Under Estimation에 큰 패널티 부여 : 예측값이 실제값보다 작을 때 더 큰 패널티 부여

추가 읽을 거리

• 왜 직관적인 MAE 말고 RMSE를 쓰나
• R-square에 대한 직관적인 이해
• 회귀 평가 지표
• 회귀 평가 지표 장단점 정리

Classification Metrics

Accuracy

• 예측한 것이 얼마나 타겟값을 많이 맞추었는지를 평가
• Unbalance 데이터셋에서 적절한 평가지표가 아닐 수 있음
• 개, 고양이 이미지 분류에서 개 10장, 고양이 90장 이미지가 있다고 가정
• 고양이 이미지는 모두 맞추고 개는 하나도 못맞췄다해도 Accuracy = 0.9
• 개를 하나도 못맞추었는데 바람직하다고 할 수 없음

LogLoss

Log Loss with Binary Classification

Log Loss with Multi-Class Classification

• Log Loss 각 클래스에 대한 예측값에 log를 씌워 계산한 것
• Cross-Entropy로도 많이 불림

AUC

Threshold(0.7)에 따른 타겟과 예측 결과

Threshold 0.7일 때의 Accuracy

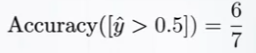Threshold 0.5일 때의 Accuracy

• Classification Model이 예측한 확률값에 어떤 Threshold를 적용하느냐에 따라 성능이 달라질 수 있음
• 위 그림에서 Threshold 0.7일 때 Green, Red 데이터들을 모두 잘 예측해냄
• Threshold 0.5라면 빨간점 1개가 Green으로 잘못 판별될 수 있음
• Threshold의 변화까지 모두 고려하여 Model의 성능 평가를 해주고자 함

Confusion Matrix 표현

• 들어가기에 앞서 예측들을 Confusion Matrix와 같이 분류 할 수 있음
• TP : Positive인 클래스들을 Positive라고 예측한 경우(위 Accuracy와 동일)
• FP : Positive인 클래스들을 Negative라고 예측한 경우
• FN : Negative인 클래스들을 Positive라고 예측한 경우
• TN : Negative인 클래스들을 Negative라고 예측한 경우

Threshold에 따른 성능 평가 : TPR = TP/(TP+FN), FPR = FP/(FP+TN)

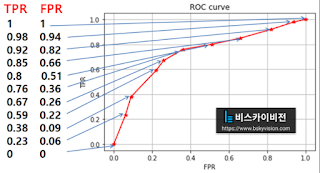Receiver Operating Characteristic(ROC) 커브

• Threshold 마다 평가한 성능을 TPR, FPR로 표현 가능
• ROC 커브 : TPR, FPR 점들로 그래프를 그린 것
• Area Under the ROC(AUC) : ROC 커브의 면적, 
• 클수록 좋은 성능 : 커브가 왼쪽 위로 치우칠수록 좋은 것
• 랜덤 예측 : 무작위로 예측 시 AUC=0.5, 즉 오른쪽 위로 향하는 대각선을 그리게 됨

Cohen's (Quadratic Weighted) Kappa

• Prediction 결과와 Target 사이의 Agreement 정도를 구하는 것
• 자세한 과정은 이 블로그를 참고하는 것을 추천드립니다(아쉽게도 영어... 지만 친절하게 단계단계 설명을 잘 해놓았습니다.)

Ranking Loss

• 주어진 데이터들을 특정 순서대로 순위를 매기는 방법이다
• 특정 클래스와 동일한 클래스는 높은 순위를, 다른 클래스들은 낮은 순위를 가지도록 학습
• 개, 고양이 이미지 분류를 한다고 가정
• 개 클래스를 선택하여 학습 시, 개 클래스 이미지들은 높은 순위, 고양이 이미지들은 낮은 순위를 가지도록 함
• Pointwise Loss

Pointwise 구하는 방법

Pointwise Loss 종류(출처)

• 1개의 데이터 입력만으로 출력 및 Loss를 구함

• Pairwise Loss

Pairwise 구하는 방법

Pairwise Loss 종류(출처)

Anchor, Positive, Negative 데이터에 따른 학습 방법

• 2개의 데이터 입력으로 출력 및 Loss를 구함
• Anchor 데이터를 기준으로 같은 Class는 Positive, 다른 Class"들은" Negative
• 개, 고양이, 말 이미지가 있다고 가정
• Anchor로 개 이미지 선정
• Positive : 개 이미지들
• Negative : 고양이, 말 이미지들(개 이미지를 제외한 모든 클래스의 이미지들)

Optimize

• Target Metric : 학습 후 Optimize 하고자 하는 대상
• Optimization Loss : 학습 과정에서 Model을 Optimize 하기 위한 것
• Loss, Cost, Objective 라고도 불림

Early Stopping 시점 : Training Loss는 줄어들지만 Validation Loss는 줄지 않고 오히려 커지는 상황(출처)

• Early Stopping : 학습 과정 중 특정 Epoch에서 학습을 멈추는 것
• 특정 시점을 어떻게 정하는 지가 핵심
• 일반적으로 Validation 성능이 더 이상 증가하지 않을 때 학습 멈춤

추가 읽을 거리

• Evaluation Metrics for Classification Problems: Quick Examples + References
• Decision Trees: “Gini” vs. “Entropy” criteria

Mean Encoding

Categorical 변수

One-hot Encoding 예시(출처)

Mean Encoding 예시 : Step-1, 2, 3 순서로 진행(출처)

• 색깔과 같은 Categorical 변수를 Machine Learning 모델의 입력으로 주기 위해서는 변환이 필요
• 이 변환 과정을 Encoding이라하며 다양한 Encoding 방법 존재
• One-hot Encoding : Category에 속하는 Dimension에만 1 나머지는 0 값을 지정한 Vector를 생성
• Mean Encoding : 각 Category마다 데이터셋 내의 타겟들의 합과 갯수들을 구하고 이들의 Mean 값으로 변환
• 다른 Encoding 방법보다 Compact하게 변환할 수 있으며 Feature Engineering에 도움이 될 수 있음
• 반대로 Overfitting 위험이 있기에 신중히 Validation 필요
• 몇몇 Dataset에 대해서만 유의미한 성능 향상이 있었다고 함

Encoding 종류

Encoding 종류와 장단점(출처)

Mean Encoding Regularization

• Mean Encoding 문제
• 위 Mean Encoding 그림에서 알 수 있듯이 Mean Encoding을 위해선 Target 값을 미리 알고 있다고 가정 필요
• 자칫 잘못하면 Test 데이터셋의 Target도 이용하여 Encoding 가능성 있음(Data Leakage)
• 또한 Train과 Test 데이터셋의 Target 분포가 심하게 다를 수 경우 Train 데이터셋의 Encoding 값이 해당 Category를 적절히 대표한다고 말하기 힘듦
• Train 데이터셋 : 남자 200명, 여자 200명
• Test 데이터셋 : 남자 10명, 여자 90명
• 위 데이터셋에서는 Encoding 값이 극명히 갈릴 수 있음
• Regularization을 도입하여 문제 해결 시도
• Regularization 종류
• Cross Validation(CV) Loop 
• CV를 통해 나누어진 Fold별로 Mean Encoding 수행
• Leave-one-out(LOO)와 같은 경우에는 조심스럽게 사용 필요
• Encoding 값이 다양해져 Tree를 만들 때 더 세분화 할 수 있다고 함
• Smoothing

Smoothing 식 : p_global=0 이면 본래 Mean Encoding과 동일(출처)

• Test 데이터셋의 Category 값들도 고려하여 Mean 값 생성
• P_global : Train, Test 데이터셋의 값들을 이용하여 구한 Mean Encoding 값
• Target 정보는 사용하지 않으니 Data Leakage에 해당하지 않음
• Noise
• Encoding 한 값에 Noise 주어 사용
• 보통 LOO와 함께 사용됨
• Expanding Mean

Cumulative Sum 예시(출처)

Expanding Mean 구현 코드

• 단순히 Sum을 활용하는 것이 아니라 Cumulative Sum을 활용
• CV Loop보다 다양한 Encoding 값을 만들어 낼 수 있음

추가 읽을 거리

• 다양한 Encoding 방법 소개
• Categorical Value Encoding 과 Mean Encoding