Deep Learning, Neural Network

Neural Net

사람의 신경망을 본따 만든 모델. 딥러닝을 접할 때 가장 먼저 듣는 얘기 중 하나 일 것이다.
이번 글에서는 왜 이렇게 얘기하는 지 알기 위해 다음과 같이 3가지를 보고자 한다.

   (1) 뉴런(Neuron)과 흡사한 퍼셉트론(Perceptron)을 살펴보고
   (2) 퍼셉트론을 이용해 어떻게 신경망(Neural Net, NN)이 만들어 지는지 본다.
   (3) 마지막으로 신경망 학습을 간략하게 살펴보고자 한다.

(용어 뒤에 영어 단어도 함께 썼는데 구글링 할 때 관련 내용을 쉽게 검색 하도록 하기 위함이다.)

1. Perceptron

사람은  뉴런이라는 신경세포로 구성된 신경계를 가지고 있다. 딥러닝 모델에서는 퍼셉트론이 뉴런에 해당한다.

[ 사람의 신경세포, 뉴런 ]

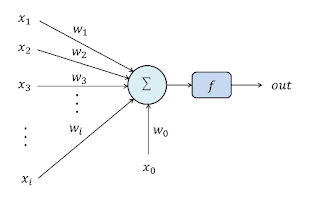
[ 단일 퍼셉트론 ]

뉴런이 동작하는 방법을 간략하게 보자면 다음과 같다. 뉴런은 가지돌기에서 전기적 신호를 받아들이는 데 각 신호마다 받아들이는 정도가 다르다. 어떤 신호는 크게, 어떤 신호는 작게 받아들일 수 있다. 그 후 이 신호가 일정 이상의 크기를 가지게 되면 다음 뉴런으로 축삭 돌기를 전기적 신호를 전달하게 된다.

[뉴런 전기 신호, threshold 이상일 때 신호 전달 됨.]

퍼셉트론은 이와 유사하게 𝑥1~𝑥i 까지의 입력 신호를 각각 w1~wi 와 곱해서 어떤 신호를 크게 받을지 작게 받을 지를 결정한다.(w는 weight의 약자로 가중치라고 한다.)  𝑥0는 바이어스인데 보통 가중치가 곱해진 입력신호에 더해져서 아래처럼 net를 구하게 된다.

[net 수식]

 net이 일정 이상의 크기를 가지면 다음 퍼셉트론으로 전달이 된다. 그림에서 ƒ로 표시된  활성화 함수(Activation Fuction)가 이 크기를 정해준다. 가장 기본적인 활성화 함수는 계단 함수(step function)으로 threshold 이상이면 출력을 낸다.

[ Step Function ]

활성화 함수는 종류 아래처럼 다양한데 sigmoid function을 많이 사용 했다가 현재는 ReLU(Rectified Linear Unit)을 많이 사용하고 있다. 신경망을 깊게 만들 수록 학습이 잘 안되는 문제(Vanishing Gradient) 때문이다. 이번 글은 뉴럴넷에 대한 소개이기 때문에 활성화 함수 및 Vanishing Gradient 문제는 다음에 다루고자 한다.

[ 활성화 함수 종류 ]

[ ReLU ]

이렇게 활성화 함수를 거치게 되면 드디어  출력(output)이 나오게 되고, 이것이 뉴런의 축삭말단에서 나오는 신호에 해당한다.

2. Multi-Layer Perceptron

a. 구조

사람의 신경계는 하나의 뉴런들이 수없이 많이 모여서 이루어진다. 사람의 뇌는 약 1000억개의 신경세포가 복잡하게 얽혀있다고 하는데 아래 그림은 최초로 뇌세포를 관찰한 결과라고 한다.

[최초 뇌세포 관찰]

퍼셉트론도 이처럼 여러개를 연결시켜 아래처럼 하나의 뉴럴넷을 만들 수 있다. 퍼셉트론이 모여서 여러 층을 이루었다고 하여 Multi-Layer Perceptron(MLP)이라고도 부른다.

[MLP]

b. Feed Forward (순전파)

위 그림에서 각각 ੦ 하나하나가 퍼셉트론이라고 보면 된다. 퍼셉트론이 아래로 쭉 쌓이면서 1개의 층을 이루고, 이를 반복하며 층을 만들어 간다. 각 층에서 쓰이는 퍼셉트론의 숫자는 임의로 정할 수 있는데 데이터가 복잡할수록 많이 쓰게 된다. 각 층을 Hidden Layer라고 부르는 데  아래 그림처럼 뉴럴넷 전체에서 보면 숨겨진 것처럼 보이기 때문이다. Feed Forward는 그림처럼 입력이 모델로 들어가 연산과정을 거치면서 출력이 나오게 되는 과정을 말한다. 마치 블랙박스처럼 모델 안에 숨겨진 layer들에 의해 연산이 진행된다.

[MLP 2]

c. Feed Forward의 결과

그러면 이 연산의 결과들은 어디에 쓰이는 것일까?

바로 " 예측 (Prediction)"에 쓰이게 된다 . 그 중에서도 어느 집단에 속하는지 예측하는 분류(Classification) 문제에 딥러닝이 자주 쓰이는 데 이는 비선형(Nonlinear)문제를 해결하는데 매우 유용하기 때문이다.

[ linear 경우, nonlinear 경우 ]

위 그림과 같이 분류를 해야 할 때 왼쪽의 경우는 굉장히 분류하기 쉽다. 그저 선 하나만 그어주면 된다.  하지만 실제로 분류를 할 때는 저렇게 잘 나눠지는 경우는 드물다. 오른쪽 그림과 같이 직선 하나로만 분류할 수 없는 문제들은 해결하기 힘들다. 그러면 사람이 직접 특징을 찾아서 위 오른쪽 그림처럼 해주면 어떨까라고 생각 할 수도 있다. 하지만 사람이 각각 데이터에 대해 모든 특징을 찾는다는 것은 힘들다. 더욱이 아래 그림과 같은 경우는 사람에게도 쉽지 않은 일일 것이다.

[ 복잡한 nonlinear 경우]

뉴럴넷은 학습을 통해 이런 비선형문제를 잘 해결해 낸다. 게다가 더 중요한 점은 학습 시킬 때 사람이 일일이 특징을 지정하지 않아도 된다는 점이다. 학습데이터만 준비하면 뉴럴넷이 스스로 특징을 학습하여 입력이 주어질 때 어떤 집단에 속하는 지 예측해 낼 수 있다. 이 때문에 신경망을 data-driven model 이라고도 불린다.

c. Softmax 함수

[Softmax 수식]

Feed Forward로 나온 값을 그대로 예측하는 결과로 사용할 수 있지만 보통 분류에서는 이 값을 Softmax함수 넣어서 나온 결과를 이용한다. 이는 Softmax가 2가지 특징을 가지기 때문이다.
   (1) Softmax의 결과의 총 합이 1이 되어서 결과를 확률로서 표현 할 수 있다.
   (2) 중요한 값을 더욱 부각 시킬 수 있다.

(2)의 특징이 중요한데 이는 아래 출처에 있는 예시를 들고와 설명하고자한다.

[Softmax 결과]

위처럼 신경망에 개 사진을 입력으로 주자. 결과로 개라고 예측한 경우는 0.9, 고양이라고 예측한 경우는 0.8, 새라고 예측한 경우는 0.7이 나왔다. 그런데 3개의 값이 비슷하다보니 확실하게 개라고 말하기 힘들다. 이 결과값을 Softmax에 넣어주면 어떤 결과가 나올까? 위 Softmax 수식을 이용해 결과값을 구해보니 개가 59%로 다른 값보다 예측값이 커져서 보다 확실하게 "개"라고 말할 수 있게 된다. 이렇게 특징되는 값을 부각시킬 수 있어서 Softmax를 사용하게 된다.

d. Back Propagation(역전파)

용어에서 볼 수 있듯이 무언가가 역방향으로 흘러간다는 뜻이다. 이 무언가가 무엇일까? 순전파일 때는 입력을 주어서 뉴럴넷을 통과 시켰다. 그러면 역으로 할 때는 과연 무엇을 주어야 할까?

[back propagation]

앞에서 순전파의 결과가 예측이라고 하였다. 그러면 이 예측이 틀리는 경우를 생각해보자. 사람이라면 틀릴 때마다 왜 틀렸는지 확인해보고 다음에는 오답율을 줄이려고 노력한다. 이 학습 과정을 여러번 반복할수록 같은 문제를 틀릴 확률이 줄어 들 것이다.  MLP도 똑같이 틀릴 때마다 확인을 해보고 오답율을 줄이기 위해 노력한다. 이를 위해 틀리는 경우 에러값을 역으로 주게 된다. 위 그림의 빨간 선이 이를 나타낸다. 에러값을 구하는 방식은 여러 가지가 있는데 평균 제곱 오차(Mean Squear Error)와 교차 엔트로피 오차(Cross Entrophy Error)를 주로 볼 수 있다. 아래와 같이 예측값이 실제값과 다른 경우 언급한 오차 구하는 방법을 이용해  오차값을 구해준다.

 

[에러 상황]

각 뉴런들은 이 에러값을 보면서 자신들의 weight 값을 수정하면서 오답율을 줄이기 위해 노력한다.  weight 값은 경사 하강법(Gradient Descent)를 이용해 수정을 한다. 아래 그림에서 J가 에러값인데 그래프의 경사도를 따라가면 에러값이 줄어드는 것을 알 수 있다. 이 과정을 학습한다라고 말한다.  이 과정이 완료 되면 앞에서 언급했던 Feed Forward를 통해 분류와 같은 예측을 할 수 있게 된다.

[gradient descent]

3. 맺음말

본 포스팅에서 사람의 뉴런을 이용해 퍼셉트론을 설명하였다. 또한 이 퍼셉트론으로 어떻게 신경망이 만들어지는지 살펴보았다. 이 신경망은 Feed Forward를 통해 예측을 할 수 있게 되며Back Propagation으로 에러율을 줄이도록 학습을 하게 된다. 소개를 목적으로 하였기에 최대한 간략이 작성하였다. 앞으로의 포스팅에서는   
   (1) 활성화 함수,  에러 구하는 방법, Back Propagation 과정 등 세부적인 내용에 대해 다루고,
   (2) 이 모델로 어떤 일을 할 수 있는 지 살펴보고자 한다.    
   (3) 마지막으로는 이 외의 뉴럴넷 모델에 대해서도 소개하고자 한다.


[ 참고 사이트 ]
- 뉴런 : https://ko.wikipedia.org/wiki/%ED%99%9C%EB%8F%99%EC%A0%84%EC%9C%84#활동전위의_각_시기
- 뇌세포 : http://blog.naver.com/PostView.nhn?blogId=wjdtkd1227&logNo=220949800053&parentCategoryNo=&categoryNo=32&viewDate=&isShowPopularPosts=false&from=postView
- 퍼셉트론 : http://untitledtblog.tistory.com/27
- 활성화 함수 : https://www.slideshare.net/ByoungHeeKim1/recurrent-neural-networks-73629152
                          http://somnode.com/dl-10/
- 뉴럴넷 역사 : https://www.slideshare.net/HyungsooRyoo/ss-80388094
- Linear, Nonlinear classification : https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/content/linear_classification.html
- nonlinear 및 PCA 등 분류 :  http://sdat.ir/en/component/k2/item/12-python-kernel-tricks-and-nonlinear-dimensionality-reduction-via-rbf-kernel-pca
- 경사하강법 : http://www.deepideas.net/deep-learning-from-scratch-iv-gradient-descent-and-backpropagation/
- Softmax : https://tensorflow.blog/%ED%95%B4%EC%BB%A4%EC%97%90%EA%B2%8C-%EC%A0%84%ED%95%B4%EB%93%A4%EC%9D%80-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-3/